Ключевые слова: динамика и качество приема студентов, показатели качественного состава профессорско – преподавательских кадров, интерактивные методы, презентации, оценка эффективности, компьютерные симуляции, профессионально — ориентированный подход.
1. Особенности преподавания
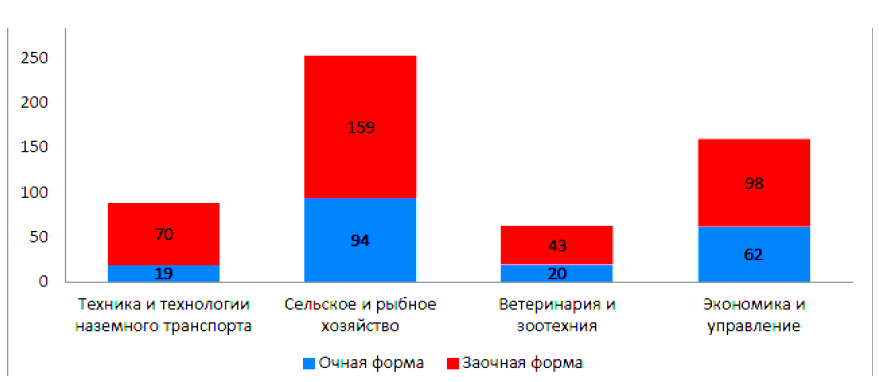
Укажем особенности преподавания математических дисциплин в ТГСХА согласно определению основных показателей учебно – методической, научной и воспитательной работы. 1.1 Динамика приёма студентов на очную и заочную форму обучения по укрупнённым группам специальностей (направлений) за 2014 год представлена на рис.1.
Имеется бюджетная и платная форма обучения. О качестве приёма студентов, зачисленных на 1 курс, свидетельствует средний балл ЕГЭ (по данным 2014 года), который на очном отделении составил 50 баллов, а на заочном – 48,6 и в целом по академии имеет тенденцию роста. Анализ приёма позволяет делать вывод об увеличении конкурса по всем направлениям.
1.2. По результатам интернет – тестирования доля студентов академии на уровне обученности не ниже второго уровня составляет 86%, что соответствует аккредитационным требованиям.
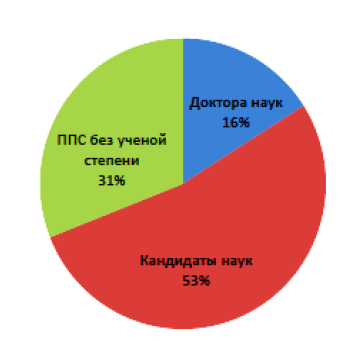
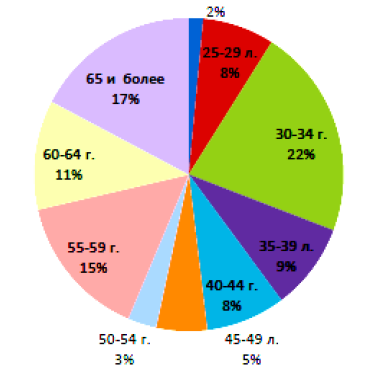
1.3. Показатели качественного состава профессорско – преподавательских кадров соответствуют аккредитационным нормативам (рис. 2, 3).
1.4. В академии организовано обучение по получению второго высшего образования. Из математических дисциплин читаются теории игр, методы оптимальных решений, эконометрика.
1.5. Введена (уже второй год) индивидуальная форма обучения.
1.6. Немалый процент обучаемых, которые недостаточно хорошо знают базовую часть школьного курса.
1.7. Все учащиеся отрицательно относятся к ЕГЭ.
1.8. Много обучается иностранных студентов из Туркмении, которые плохо знают русский язык.
1.9. Широкое использование компьютерного тестирования при оценке знаний. Обучаемые по – разному относятся к такой форме контроля, примерно, 20 – 30 % предпочитают ответ по билетам и беседу с преподавателем.
1.10. По всем математическим дисциплинам, связанным с разного рода моделированием (игровым, эконометрическим, статистическим, вероятностным, экономико – математическим), все занятия проводятся в компьютерных классах, на многих лекциях используются презентации. Работа в компьютерных классах нравится всем обучаемым. Что же касается презентативной формы чтения лекций, то здесь мнения разделились в соотношении: 50% за эту форму, 50% — против, т.е. предпочтение отдают чтению лекций по – старинке, когда учащиеся пишут излагаемый математический материал «за рукой преподавателя». По мнению многих преподавателей математики ТГСХА наиболее рациональной является такая форма чтения лекций, когда презентации составляют 5 – 10 кадров, представляющих собой систематизированное изложение большого информативного материала, представленного объёмными таблицами, графиками, громоздкими математическими выражениями. Однако, такие презентации имеют весомое значение лишь только в том случае, если будут продублированы раздаточным материалом, который раздаётся обучаемым перед лекцией, а затем вклеивается в конспект. Опорный конспект по – прежнему играет ведущую роль в формировании знаний.
1.11. В процесс обучения по математическим дисциплинам внедрены разработанные автором инновационные технологии обучения, связанные с классификацией обучаемых по группам успеваемости на основе байесовского правила [1], эконометрическими моделями показателей качества учебного процесса [2], синергетическим эффектом объединения признаков в сложной системе организационного управления [3], оценкой эффективности учебно-воспитательного процесса в вузе [4], оценкой качества учебно-тематического плана [5], системным подходом к процессу получения и формирования знаний [6], организацией сбалансированной работы учащихся [7], определением оптимальных модулей и компетентности обучаемых [8], сетевым планированием и управлением формированием компетенций [9], интеллектуальной информационной системой оптимального контроля знаний [10], учебными динамическими сценами [11].
Нужна помощь в написании статьи?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Пишем статьи РИНЦ, ВАК, Scopus. Помогаем в публикации. Правки вносим бесплатно.
1.12. Широкое использование интерактивных методов (мозговой штурм, ромашка, разбор ситуаций, дискуссия, кейс – метод). Вовлечение в игру, например, использование интерактивного метода «Морской бой».
1.13. Большое внимание на лекциях и практических занятиях уделяется патриотическому воспитанию. Для разрядки на занятиях и лекциях преподаватель делает 5 – ти — минутные сообщения из истории развития математики, о выдающихся учёных, прежде всего отечественных учёных. Такие сообщения могут делать и сами учащиеся. Это воспитывает чувство гордости, кроме того, учащиеся проникаются сознанием того, что для достижения цели надо много работать, путь к вершине «не усыпан розами», должна быть одержимость, непреодолимое желание к свершениям. И они это тоже смогут, если только очень — очень захотят.
1.14. В академии существуют различные научные студенческие кружки (в том числе по математическим дисциплинам), на которых рассматриваются вопросы, связанные с математическим моделирование экономических задач, проблемами растениеводства, животноводства, моделированием бытовых ситуаций. Например, имеется кружок по тематике – «Применение математических методов в социально – производственной сфере».
2. Пути повышения качества преподавания
Перечислим основные пути повышения качества преподавания на примере ТГСХА.
2.1. Прежде всего должен быть профессионально – ориентированный подход, заключающийся в использовании прикладных задач предметной области специализации. Для этого следует сделать анализ прикладных задач, провести их типизацию, определить требования, предъявляемые к учебным прикладным задачам, составлению методики решения и исследования прикладных задач в учебном процессе. Следует отметить значение прикладных задач в курсе математики для повышения интереса к обучению. Поиск прикладной задачи является творческим процессом. Он начинается с внимательного изучения учебной литературы по специальным и общетехническим дисциплинам с целью выявления профессиональной задачи, для решения которой целесообразно построить математическую модель, решение которой и анализ этого математического решения позволяют сделать практические выводы. При этом методика решения построенной модели должна существенным образом иллюстрировать изучаемый в данный момент раздел математики и убеждать студентов в необходимости математического образования для более глубокого овладения профессией.
Требования к прикладной задаче сформулированы в [12]. Это прикладные экономические задачи, возникающие при работе агрофирм, коммерческих предприятий, информационных, торговых, транспортных, энергетических систем. На практических занятиях разбираются математические задачи, с которыми будут встречаться на практике агрономы, зооинженеры, механизаторы.
2.2. Развитие интереса – главная движущая сила учебного процесса. Профессионально – ориентированный подход стимулирует эту силу. Ещё один толчок этому стимулированию даёт процесс привлечения наиболее способных студентов к научно – исследовательской работе уже на первом курсе. Кроме того, одной из основных составляющих развития интереса и своеобразной «разрядки» являются задачи юмористического характера, в частности, из социально – бытовой сферы. Например, векторные модели музыкальных произведений, характеров людей, кулинарных блюд [13].
2.3. Как показывает опыт преподавания математических дисциплин, связанных с различного рода моделированием, — эконометрики, теории игр, теории вероятностей, статистики, экономико – математического моделирования – очень продуктивным является использование на практических и лабораторных занятиях метода компьютерных симуляций, представляющих собой пошаговую компьютерную алгоритмизацию решения задач, сводящуюся к работе с компьютером – репетитором [14]. Студенты с большим энтузиазмом и интересом осваивают такой материал. Неплохо было бы использовать этот опыт на практических занятиях и по таким дисциплинам, как математика у менеджеров, инженеров, на технологическом факультете, линейная алгебра, математический анализ (экономисты), специальные главы математики и прикладная математика (инженерный факультет).
2.4. Одна из возможных реализаций оптимального овладения компетенциями – шире привлекать самих студентов к решению этой задачи. Так, в ТГСХА при изучении курса математического анализа для реализации компетенций ПК – 14, ПК – 15, направленных на ознакомление студентов с учебно – методической работой преподавателя, выделилась группа студентов, которые по собственному желанию стали участвовать в подготовке учебно – методического обеспечения: совершенствовали под руководством преподавателя макеты программ, научились по программам записывать тематические планы, практиковались в разработке интерактивного метода «Ромашка», трое студентов под руководством преподавателя прочитали лекции с упором на применение математического аппарата в экономической сфере.
2.5. По – прежнему очень актуальным для оптимизации процесса обучения является дифференцированный подход к обучаемым. В соответствии с их математической подготовкой на предшествующих ступенях обучения, учащимся предлагаются индивидуальные задания, оценённые по соответствующей балльной шкале.
2.6. Тесный контакт с учащимися – залог успеха. На лекциях, на практических (лабораторных) занятиях, в учебное и не учебное время необходим тесный контакт преподавателя с учащимися. Во время чтения лекций и проведения занятий широко используются активные (общение преподавателя с учащимися) и интерактивные ( общение преподавателя с учащимися и учащихся друг с другом) методы. Необходимо шире использовать такие методы как «Дискуссия», «Разбор ситуаций», «Морской бой», «Интеллектуальный футбол». Это способствует развитию интереса, индивидуальной и коллективной творческой мысли, способности принимать решения, обосновывая их. Периодически на лекциях и занятиях преподаватель должен уделять немного времени воспитательным беседам по развитию патриотизма (гордость за отечественную науку и её представителей). Во время консультации преподаватель не только объясняет непонятные моменты, принимает «отработки», но и старается вникнуть в проблемы каждого учащегося, чтобы рационально организовать учебный процесс.
2.7. Негативное отношение к математике, сложившееся, к сожалению, у некоторых обучаемых ещё в школьных стенах, нейтрализуется, например, экскурсом в историю развития математики и примерами из жизни и творчества учёных – математиков, а также вовлечением таких студентов в исследовательскую работу по решению некоторых несложных бытовых ситуаций типа: влюблённый юноша должен в кратчайшее время добраться до пункта, где проживает девушка, или решение конфликтных семейных ситуаций и т. п.
2.8. Рейтинговая система обучения во многом является мобилизующим рычагом активизации и повышения качества процесса обучения. Как показывает опыт, все студенты стараются получить побольше баллов во время учебного процесса. Пропущенная часть лекций и занятий обрабатывается (часто по инициативе самих студентов), часть студентов ходатайствуют о дополнительных индивидуальных заданиях для лучшего усвоения учебного материала.
2.9. Шире использовать перечисленные в §1 инновационные технологии.
Список использованных источников
1. Ганичева А.В. Использование классификации обучаемых по группам успеваемости для повышения эффективности учебного процесса // Актуальные вопросы современной науки: сб. науч. тр. 7–ой межд. ИНТЕРНЕТ-конф. Таганрог. М: Изд-во «Спутник+», 2010. С. 23-27.
2. Ганичева А.В. Эконометрические модели показателей качества учебного процесса // Материалы Всерос. науч. конф., вып. 9. Тверь: ТГТУ, 2009. С. 197-204.
3. Ганичева А.В. Синергетический эффект объединения признаков в слож-ной системе организационного управления // Синергетика в естественных науках: материалы межд. междис. науч. конф. Пятые Юбилейные Курдюмовские чтения, Тверь: ТГУ, 2009. С. 328-333.
4. Ганичева А.В. Модели оценки эффективности учебно-воспитательного процесса в вузе // Журнал научных публикаций «Дискуссия». Тематический выпуск «Инновации гуманитарных и естественных наук». Екатеринбург: УГТУ, 2010. С.
5. Ганичева А.В. Методика оценки качества учебно-тематического плана // Образования в 21 веке: материалы всерос. конф., вып. 11. Тверь: ТГТУ, 2011. С.82-87.
6. Ганичева А.В. Системный подход к процессу получения и формирования знаний // В мире научных открытий. Серия «Математика. Механика. Информатика». 2011. №112. С. 83-102.
7. Ганичева А.В. Организация сбалансированной системы самостоятельной работы учащихся // Синергетика в естественных науках: материалы межд. междис. науч. конф. Восьмые Курдюмовские чтения, Тверь: ТГУ, 2012. С. 260-263.
8. Ганичева А.В. Метод определения оптимальных модулей и компетентности обучаемых // Качество. Инновации. Образование. 2013. №10. С. 19-23.
9. Ганичева А.В. Сетевое планирование и управление формированием компетенций и компетентности // Вестник Тверского государственного университета. Серия: Педагогика и психология». 2014. Вып. 3. С. 81 – 90.
10. Ганичева А.В. Интеллектуальная информационная система оптимального контроля знаний // Политем. сетевой электр. науч. журнал Кубанского государственного аграрного университета (Научный журнал Куб-ГАУ) [Электронный ресурс]. Краснодар: Куб-ГАУ. 2014. №07(101). IDA [article ID]: 1011407019. Режим доступа: http://ej.kubagro.ru/2014/07/pdf/19.pdf
11. Ганичева А.В. Учебные динамические сцены // Научно-образовательная информационная среда XXI века». Петрозаводск, 15 — 18 сентября 2014 года. С. 42 – 46
12. Ганичева А.В. Профессионально – ориентированный подход к преподаванию математических дисциплин в сельскохозяйственных вузах // Инновационные образовательные технологии и методы их реализации в формате ФГОС ВПО: сб. тр. Всерос. науч. – метод. конф., Тверь: Тверская ГСХА, 2014. С. 193 – 196.
13. Ганичева А.В. Развитие интереса – движущая сила учебного процесса // Инновационные образовательные технологии и методы их реализации в формате ФГОС ВПО: сб. тр. Всерос. науч. – метод. конф., Тверь: Тверская ГСХА, 2014. С. 200 – 203.
14. Ганичев А.В. Интерактивное учебное занятие по математической статистике // Инновационные образовательные технологии и методы их реализации в формате ФГОС ВПО: сб. тр. Всерос. науч. – метод. конф., Тверь: Тверская ГСХА, 2014. С. 203 – 208.
Нужна помощь в написании статьи?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Пишем статьи РИНЦ, ВАК, Scopus. Помогаем в публикации. Правки вносим бесплатно.